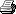qazwsxedc - Sob 11 Gru, 2010 Temat postu: pytanie z optyki Nurtuje mnie pewien problem związany z GO, wielkością matryc i wartości.a przysłony w obiektywie. Np mam obiektyw o ogniskowej 100mm podpięty do aparatu FF i mam obiektyw 50mm podpięty do aparatu z matryca 4/3. Więc mam ten sam kąt widzenia czyli robiąc zdjęcie z tej samej odległości dostane dwa identyczne kadry (ta sama perspektywa). Ale żeby uzyskać ta samą GO to obiektyw na FF musi mieć wyższa przysłonę o wartość croppa. Np 100mm/16 (FF) będzie odpowiadać 50mm/8 (4/3). Wtedy otwór bezwzględny przysłony jest identyczny. I teraz pytanie czemu tak jest? Czemu GO zależy fizycznego otworu przesłony w przypadku tej samej perspektywy i kadrów a różnej wielkości matrycy? Bardzo chciałbym poznać takie fizyczne uzasadnienie, jakiś dowód. Próbowałem to sobie rozrysować tak jak się rysuje soczewkę z różnymi wartościami przysłony tworzącą obraz na matrycy. Wtedy widać, że zmieniają się kąty i to wpływa na GO. Ale nie wiem jak to zrobić dla różnych matryc. Bardzo proszę o pomoc w tej sprawie. Jeśli to zły dział to przepraszam, ale nie wiem jaki byłby odpowiedniejszy? hijax_pl - Sob 11 Gru, 2010 qazwsxedc, poczytaj o krążkach rozproszenia. I jak się to przekłada na wielkość matrycy qazwsxedc - Sob 11 Gru, 2010 hijax_pl czytałem o krążkach rozproszenia. Ale nie widzę jak z analizy wielkości krążków rozproszenia wynika zależność o którą pytam: stała bezwzględna wielkość otworu przysłony przy różnych formatach matrycy daje tą sama GO (pod warunkiem, że perspektywa i kadr są identyczne). Jeśli wiesz jak to udowodnić to proszę napisz. hijax_pl - Sob 11 Gru, 2010 qazwsxedc, troszkę się rozpędziłem.
Głębia ostrości jest niezależna od konstrukcji obiektywu. Zatem przy Twoim przykładzie różnice będą tylko w dopuszczalnych krążkach rozproszenia, zakładając wykonanie odbitek o tej samej wielkości. qazwsxedc - Sob 11 Gru, 2010 To może zapytam inaczej. Czemu GO zależy właśnie od bezwzględnej wielkości przesłony? Jeśli mamy ten sam obiektyw z tą samą matrycą i jedynie zmieniamy wartość przysłony, to zmieniają się kąty pod jakimi padają promienie na matryce i ładnie widać zmianę GO. Na wiki jest taki obrazek: http://upload.wikimedia.o...tration.svg.png Ale jak to się ma do tej sytuacji którą opisałem: 100mm/16 na FF i 50mm/8 na 4/3? Przecież dłuższa ogniskowa to większa odległość obiektyw-matryca. Czyli kąty pod jakimi padają promienie powinny być takie same dla 100mm/8 (FF) i 50mm/8 (4/3). 100mm/8 ma fizycznie 2x większy otwór niż 50mm/8 ale tez odległość obiektyw-matryca jest 2x większa. Po prostu nie wiem jak udowodnić albo jakoś pokazać na rysunku z soczewką i matrycą, że dla 100mm/16 (FF) i 50mm/8 (4/3) Go będzie takie samo. TS - Sob 11 Gru, 2010
Patrząc na podlinkowany rysunek widzę sprawę następująco. Ten sam bezwględny rozmiar otworu da Ci takie ugięcie promieni. Na FF odległość soczewki od matrycy masz 2x większą, zatem krążek rozproszenia będzie też 2x większy. Ponieważ sensor jest 2x większy, to procentowo krążek zajmie tyle samo miejsca, czyli GO będzie taka sama. Ale sam się chętnie dowiem jak to jest, bo nie mam pojęcia o optyce, to dla mnie wynika z rysunku... Do tej pory wystarczał mi wzór, nie wnikałem skąd on jest (co oczywiście jest ciekawe, tylko trzeba mieć na to czas hijax_pl - Sob 11 Gru, 2010
Wrócę znów do tych nieszczęsnych krążków. Domykanie przysłony powoduje , że nam się te stożki wyciągają (zmniejsza się kąt wierzchołkowy) - czyli średnice w punkcie przecięcia z płaszczyzną obrazową są coraz mniejsze. A to prowadzi do wniosku, iż bliżej nam do tych krytycznych wielkości krążków uznawanych za ostre. Zauważ jaki wpływ ma odległość przedmiotowa - im mniejsza tym coraz większy kąt wierzchołkowy stożków. W szczególności, proste biegnące z nieskończoności są "praktycznie równoległe", dając obraz ostry niezależnie od użytej przysłony. Co do porównywania wielkości matryc może prościej będzie wyobrazić sobie to w ten sposób: masz aparat FF, obiektyw np 100mm i użytą przysłonę np f/5.6. Robisz zdjęcie - dla uproszczenia niech będzie to negatywowa klisza, z którego wykonujesz odbitkę w formacie 20x30cm. Co jest krążkiem rozproszenia? Ano to co widzisz na wydruku jako punkt. A teraz zmieniamy nastawy powiększalnika tak aby na papierze 20x30cm znalazła się tylko środkowa część kadru (powiększamy dwukrotnie). I co się okazuje? Powiększamy krążki. To co wcześniej było ostre zaczyna wchodzić nam w nieostrość. Taki sam eksperyment - ale myślowy można przeprowadzić w drugą stronę. Tym razem zmniejszamy obraz dwukrotnie, tak aby oryginalna klatka FF weszła nam w obszar APS-C (czyli zmniejszamy dwukrotnie). Zauważamy, że więcej elementów jest ostrych - i tak też jest; dwukrotne pomniejszenie spowodowało, że głębia się dwa razy zwiększyła. I tak też się dzieje, gry porównujemy kadry FF i APS-C. Jeśli mamy to samo odwzorowanie - mamy tą samą głębię (ale inne kadry). Jeśli mamy takie same kadry, to mamy inne odwzorowanie i zarazem inną głębię. qazwsxedc - Nie 12 Gru, 2010 hijax_pl z matrycy 4/3 powiększasz obraz 2x bardziej niż z FF aby otrzymać taki sam wydruk. Czyli w myśl Twojego rozumowania to obrazy z mniejszej matrycy będą miały większą GO, a przecież jest odwrotnie. Poza tym APS-C nie jest 2x razy mniejsze od FF, coś Ci się miesza. dr11 - Nie 12 Gru, 2010 qazwsxedc, pooglądaj, poczytaj... http://canon-board.info/showthread.php?t=35157 http://canon-board.info/s...8&postcount=461 qazwsxedc - Nie 12 Gru, 2010 dr11 ja już kiedyś przeglądałem forum canonowców ale tam konkretnej odpowiedzi nie znalazłem. Praktyczne różnice między formatami znam. Ale jak narysować sobie te promienie przechodzące przez soczewkę i padające na matryce w obu przypadkach tak żeby było widać odpowiednie kąty i ich wartości to nie wiem. A właśnie to by wytłumaczyło wszystko. Pytanie nie jak jest ale dlaczego jest właśnie tak! dr11 - Nie 12 Gru, 2010 qazwsxedc, tu wszystko ustawisz, zobaczysz jak się mają obrazy do długości ogniskowej, wielkości otworu, jedynie zmianę wielkości sensora musisz sobie wyobrazić. http://phet.colorado.edu/...-optics_en.html qazwsxedc - Nie 12 Gru, 2010 dr11 fantastyczną stronę podałeś. Na prawdę znakomity symulator soczewki. Co prawda nadal nie wiem czemu o GO decyduję bezwzględna wielkość otworu przysłony. Próbowałem to dzisiaj cały dzień sobie narysować i policzyć i nic. Może jutro się uda hijax_pl - Nie 12 Gru, 2010
FF - 36x24mm = 864mm² APS-C (Nikona) - ok 23.6x15,7mm = ok 370mm² 4/3 - 17.3x13mm = 225mm² Czyli 4/3 do FF ma się tak 225/864 = 0,26 albo inaczej 864/225=3,84. Wynika z tego że powierzchniowo FF jest prawie 4x większa od 4/3.
qazwsxedc - Nie 12 Gru, 2010
Ale potem ten pomniejszony obraz (z FF do 4/3) musisz bardziej powiększyć żeby uzyskać wydruk np a4. Najpierw pomniejszasz 2x a potem powiększasz o 2x bardziej niż powiększałbyś obraz z matrycy FF.
Ale trzeba porównywać przekątne a nie powierzchnie matryc
Nie myli mi się:) Poza tym jeśli nie znasz odpowiedzi na moje pytanie to nie mieszaj. Proszę. ps prawdopodobnie odpowiedź na moje pytanie jest w książce Stroebel - może ma ją ktoś w pdf? hijax_pl - Nie 12 Gru, 2010

hydra - Nie 12 Gru, 2010
Jeżeli chodzi Ci o The Focal encyclopedia of photography to pod tym adresem są jej obszerne fragmenty http://books.google.pl/bo...epage&q&f=false qazwsxedc - Pon 13 Gru, 2010 hijax_pl ten rysunek pokazuje, że GO zależy od kąta stożka światła padającego na matryce. Przy tym samym otworze bezwzględnym i różnych ogniskowych stożek będzie węższy dla dłuższej ogniskowej. Czyli GO dla krótszej ogniskowej będzie większe. Ale jeśli oba obiektywy będą mieć taką samą wartość przysłony, to te stożki będą miały taki sam kąt. Przecież wartość przysłony jest wartością liczoną względem ogniskowej. 100mm/8 i 50mm/8 będą dawać stożek o takiej samej wielkości kątowej. Po prostu nie wiem jak uwzględnić wielkość matrycy. hydra o tej książce nie słyszałem. Chodziło mi o "View Camera Technique" hijax_pl - Pon 13 Gru, 2010
qazwsxedc - Wto 14 Gru, 2010
I co z tego wynika? hijax_pl - Wto 14 Gru, 2010 Na rysunku są dwie soczewki. Potraktujmy je jako obiektywy o ogniskowych A:100mm i i B:50mm. Otwór względny jest taki sam, powiedzmy liczby przysłony będą f/5.6 dla A i f/2.8 dla B (da to nam otwór o średnicy 17,86mm) Z rysunku wynika, że GO w przypadku B jest większa. Policzmy: korzystając z kalkulatora możemy sobie policzyć GO dla kliszy 135mm (wymuszamy sobie krążek rozproszenia) i odległości przedmiotowej 5m: - dla A będzie to 0,84m - dla B będzie to 1,73m Jeśli ustawimy tą samą wartość przysłony, np f/5.6 na obu obiektywach: - dla A będzie to 0,84m - dla B będzie to 3,79m Co prawda policzyliśmy sobie odległości na kalkulatorze, ale spójrz jeszcze raz na rysunek. To jak ogniskowa wpływa na odległości obrazowe dla tych samych odległości przedmiotowych. Na upartego można usiąść i policzyć je sobie z równania soczewki: 1/f = 1/x + 1/y Wracając do rysunku. Promienie, które będą dawały ostry obraz muszą się przecinać z osią optyczną w takiej odległości od ogniskowej, aby utworzony w ten sposób kąt wierzchołkowy stożka nie był większy od założonego przez nas kryterium ostrości. To czy to będzie 1nm czy 1km - nie ma tu żadnego znaczenia. Zauważ, że rysunek przedstawia sytuację w której mamy dwa różne odwzorowania. Czyli różne odwzorowanie to różne GO. Aby uzyskać tą samą GO - musimy zmienić odległość przedmiotową by utrzymać to samo odwzorowanie. Oczywiście oznacza to zmianę perspektywy. A teraz wplatamy matrycę. Matryca to nic innego jak jakaś powierzchnia ułożona w odległości ogniskowej. To czy ona ma powierzchnię klatki 35mm czy też jest mniejsza - nie ma dla optyki żadnego znaczenia. Załóżmy, że wykonana jest w sposób dający nieskończoną rozdzielczość oraz, że docelowym formatem odbitki, który nas interesuje jest format 20x30cm - bo przecież chcemy oceniać różnice oglądając dwa zdjęcia Wykonujemy zatem powiększenie: - w przypadku matrycy FF (36x24mm) - 8,3x - w przypadku matrycy APS-C (23.6x15.7mm) - 12,7x Przyjmijmy, że oglądając odbitkę, za ostre uznajemy elementy mniejsze od 0.1mm. Wynika z tego, że kryterium ostrości będzie: - w przypadku matrycy FF - 0.012mm - w przypadku matrycy APS-C - 0.0079mm Te wartości to graniczne średnice podstaw stożków w płaszczyźnie ogniskowej dających ostry, czyli "punktowy" obraz. Wysokość stożków dyskryminuje nam głębie ostrości, czyli dopuszczalny zakres "odchyłek" odległości tworzenia obrazu od odległości ogniskowej (czyli odległości między planami I', II' i III' od F'). Operujemy tu w dziesiątych częściach milimetra, ale korzystając znów ze wzoru soczewki, możemy GO przedstawić jako zakres "odchyłek" od odległości przedmiotowej. Patrząc na wartości kryterium ostrości dla różnych matryc można zauważyć, że przy okazji otrzymaliśmy informację o największym możliwym rozmiarze piksela, dla którego uznamy obraz za ostry. Zmniejszanie go umożliwi nam wykonywanie większych odbitek przy zachowaniu tej samej głębi ostrości. Podsumowując, głębia ostrości zależy od ogniskowej i otworu względnego oraz arbitralnie przez nas obranego kryterium - krążka rozproszenia. Czy to można potraktować jako odpowiedź na Twoje pytanie? B o g d a n - Wto 14 Gru, 2010
hijax_pl - Wto 14 Gru, 2010 B o g d a n, to ja w takim razie nie rozumiem problemu qazwsxedc. jaad75 - Sro 15 Gru, 2010 hijax_pl, generalnie chodzi o to, z czego wynikają ekwiwalenty ogniskowej i GO, dla poszczególnych formatów i jak sobie to rozrysować. Dlaczego np. 50-tka @f/2.8 na 4:3 jest ekwiwalentem 100@f/5.6 na FF? Jak dla mnie wynika, to tylko z przyjętej wartości krążka rozproszenia, ale może coś przeoczyłem - jakoś nigdy nad tym się głębiej nie zastanawiałem... qazwsxedc - Sro 15 Gru, 2010
Niestety też tak myślę. [ Dodano: Sro 15 Gru, 2010 15:23 ]
Może jakiś mało rozgarnięty jestem ale mi to z krążków rozproszenia nie wynika. Może znajdzie się ktoś, kto to wszystko ładnie poukłada i zniknął wątpliwości hijax_pl - Sro 15 Gru, 2010 
n - przysłona (wyrażona w liczbie) f - odległość ogniskowa (mm) x - odległość przedmiotowa (mm) y - odległość obrazowa (mm) d - krążek rozproszenia / podstawa stożka z - wysokość stożka (mm) α - kąt wierzchołkowy Dla pewnych uproszczeń przyjmijmy, że średnica otwory przysłony jest podstawą stożka padania promieni światła. A soczewka to... soczewka cienka. Dla treningu przeliczmy sobie średnicę krążka 'd' przy następujących danych: f = 100mm n = f/5.6 x = 7m Wielkość otworu przysłony to f/n=100/5.6=17.86mm. Z równania soczewki 1/f=1/x+1/y wyznaczamy y=101.45mm, z trygonometrii natomiast kąt α (trójkąt będzie miał wysokość 'y' i podstawę 'n') = 10.06°. Mając kąt - możemy wyznaczyć średnicę podstawy stożka 'd' w miejscu przecięcia z płaszczyzną ogniskową 'f'. Wyjdzie nam 0.25mm. Czyli punkt leżący w odległości x=7m tworzy plamkę o średnicy 0.25mm. Odpowiednio dla: x=10m będzie to plamka o średnicy 0.18mm, natomiast dla x=3m plamka będzie wielkości 0.59mm To teraz wracamy do matrycy. Załóżmy, że z obu aparatów robimy to samo ujęcie o rozdzielczości np: 12 Mpix, które oglądamy na tym samym monitorze. Przyjmujemy, że ostre jest to co na matrycy pełnoklatkowej jest plamkami nie większymi niż 0,03mm - bo tak się przyjmuje i już Matryca pełnoklatkowa ma rozmiar 36x24mm i przekątną 43.27mm. Matryca 4/3 odpowiednio 17.3x13mm i przekątną 21.64mm Matryca 4/3 jest mniejsza od pełnoklatkowej dokładnie 43.27/21.64=1.99x. Jest to nasz współczynnik powiększenia. Ponieważ oglądając zdjęcie na komputerze powiększamy je dwa razy bardziej w porównaniu do zdjęcia pełnoklatkowego - musimy zmienić dopuszczalny krążek rozproszenia, czyli 0,03/1.99=0.015mm Ale mniejsza matryca to też inny kąt widzenia. Aby uzyskać ten sam kadr musimy użyć innej ogniskowej. Możemy ją sobie wyliczyć z trygonometrii, lub po prostu podzielić ogniskową użytą na aparacie pełnoklatkowym przez współczynnik powiększenia. Czyli 100/1.99=50mm Jeśli nie zmienimy przysłony (nadal f/5.6), na matrycy 4/3 i obiektywie f=50mm uzyskamy następujące plamki: x=10m będzie to plamka o średnicy 0.04mm, natomiast dla x=7m plamka będzie wielkości 0.06mm, oraz dla x=3m plamka będzie wielkości 0.15mm. Chcąc mieć ten sam otwór bezwzględny przysłony (czyli 17,86mm) na obiektywie 50mm musimy go bardziej otworzyć. Dokładnie do 50/17.86=2.8. Przy takiej konfiguracji obiektywu plamki będą miały następujące wymiary: x=10m będzie to 0.089mm, natomiast dla x=7m plamka będzie wielkości 0.13mm, oraz dla x=3m plamka będzie wielkości 0.29mm. Powiększy sobie teraz tę klatkę do rozmiaru 36x24mm, czyli przemnóżmy nasze plamki przez współczynnik powiększenia równy 1.99, odpowiednio dla: x=10m będzie to 0.18mm, natomiast dla x=7m plamka będzie wielkości 0.25mm, oraz dla x=3m plamka będzie wielkości 0.59mm. Otrzymaliśmy takie same plamki co na aparacie FF z obiektywem 100mm i przysłoną ustawioną na f/5.6 [ Dodano: Czw 16 Gru, 2010 09:49 ] Dodatek: Próba przedstawienia tego co policzyłem powyżej w formie graficznej 
Kolor niebieski: obiektyw 100mm f/5,6 Kolor czerwony: obiektyw 50mm f/2,8 Kolor zielony: odległość ogniskowa dla obu obiektywów - Dla tej samej odległości przedmiotowej punkty przecięcia z osią optyczną będą w różnych miejscach dla różnych ogniskowych. Co dokładnie widać na powiększeniu. - Dla czerwonego obiektywu płaszczyzna odległości obrazowej (punkt przecięcia z osią) jest bliżej płaszczyzny ogniskowej (zielonej)w porównaniu do niebieskiego obiektywu. - Na powiększeniu widać też, że podstawa stożka w płaszczyźnie ogniskowej (zielonej) jest większa dla niebieskich promieni niż czerwonych mimo, że kąt wierzchołkowy dla czerwonych promieni jest większy od tego dla niebieskich. - ponieważ mówimy też o dwóch różnych matrycach (4/3 vs FF) mamy dwa różne kryteria ostrości - co przekłada się na maksymalną dopuszczalną średnicę podstawy stożka. Wniosek - przy zachowaniu tej samej perspektywy (odległość przedmiotowa), kąta widzenia obiektywu (ogniskowa i wielkość matrycy) oraz bezwzględnego otworu przysłony otrzymamy identyczne kadry z identyczną głębią ostrości. k33l - Czw 16 Gru, 2010
Zmienia się ogniskowa ale czy zmienia się też światło? Oczywiście ogniskowa się nie zmienia bo jest stała dla obiektywu (w zoomie jest zmienna ale rozmiar matrycy jej nie zmienia) zmienia się kąt widzenia obiektywu przez to że właśnie matryca jest innego rozmiaru, tak naprawdę to obiektyw 50mm Olympusa to ekwiwalent takiego obiektywu na FF, ma taki kąt widzenia jak 50mm na FF ale fizycznie to nie jest to obiektyw 50mm. Często na kompaktach widać że mają ogniskowe np. 6mm-20mm i dopisek jaki jest to ekwiwalent dla małego obrazka. Dla 4:3 obraz to wycinek z FF i daje złudzenie że ogniskowa jest dłuższa. komor - Czw 16 Gru, 2010 jaad75, tak prewencyjnie proszę o umiar i litość. hijax_pl - Czw 16 Gru, 2010 komor, pantaksiarze się przecież nie pobiją k33l - Pią 17 Gru, 2010 hijax_pl kim są "pantaksiarze"? hijax_pl - Pią 17 Gru, 2010
Jakby nie patrzeć to te liczny są różne. Zatem chiba tak - zmienia się światło jaad75 - Pią 17 Gru, 2010 k33l, weź przeczytaj jeszcze raz, o czym mowa i pomyśl przed następnymi wynurzeniami...
nugat - Sob 18 Gru, 2010 Temat postu: DOF, CoC & Airy Disk Chyba jednak krążek rozproszenia (CoC)... Dobre tutoriale: http://www.cambridgeincol...th-of-field.htm http://www.cambridgeincol...photography.htm Jest też oryginalne, dogłębne i ciekawe podejście do tematu Harolda Merklingera: http://jimdoty.com/learn/...k/dof_merk.html hijax_pl - Sob 18 Gru, 2010
cybertoman - Sob 18 Gru, 2010
jaad75 - Sob 18 Gru, 2010 cybertoman, jak 50mm@f/2.8 na 4:3. hijax_pl - Sob 18 Gru, 2010
Ten sam otwór bezwzględny to np: 200mm f/11.2 -> 200/11.2=17.86mm 100mm f/5.6 -> 100/5.6=17.86mm 50mm f/2.8 -> 50/2.8=17.86mm nugat - Sob 18 Gru, 2010
"chyba" jak "chyba??!!", czyli żart. Niechybnie. qazwsxedc - Pon 27 Gru, 2010 hijax_pl dzięki za pomoc. To co napisałeś ma faktycznie sens. Dla tej samej odległości przedmiotowej odległość obrazowa jest mniejsza dla krótszej ogniskowej a dla dłuższej jest większa. Jak to wpływa na CoC to ładnie pokazałeś na rysunku. 
Ale mam nadal jedno pytanko, w jakiej odległości dokładnie jest matryca? Bo od tego bardzo dużo zależy. Gdyby ją odsunąć bardziej od soczewki to GO by spadła. hijax_pl - Pon 27 Gru, 2010
Powiem więcej: kiedy odległość przedmiotowa jest nieskończona (czyli 1/x dąży do zera) wtedy odległość obrazowa jest równa odległości ogniskowej, czyli na pytanie:
Mogę tylko powiedzieć, że obiektywy klasyczne (czyli takie bez wewnętrznego ogniskowania) wysuwają się (czyli de facto zwiększają odległość od matrycy) właśnie po to by ostrzyć na mniejsze odległości. Czy to Ci pomoże w rozważaniach? Nie wiem... GoOrange - Pon 27 Gru, 2010 hijax_pl, Generalnie chylę czoła... cybertoman - Czw 30 Gru, 2010
hijax_pl - Czw 30 Gru, 2010
jaad75 - Czw 30 Gru, 2010
cybertoman - Czw 30 Gru, 2010
[ Dodano: Czw 30 Gru, 2010 11:14 ]
[ Dodano: Czw 30 Gru, 2010 11:16 ]
hijax_pl - Czw 30 Gru, 2010
A to jest złe uogólnienie? cybertoman - Czw 30 Gru, 2010
hijax_pl - Czw 30 Gru, 2010 A dlaczego? Brakuje odniesienia do wielkosci odbitki? cybertoman - Czw 30 Gru, 2010 Wniosek sugeruje, ze tak jest zawsze, a wystarczy przeliczyc dla odleglosci przedmiotowej blizszej ogniskowej, by sie przekonac, ze tak nie jest (np. 20 cm). hijax_pl - Czw 30 Gru, 2010 cybertoman, no chyba jasnym jest, że rozpatrujemy tylko i wyłącznie przypadek używany w fotografii amatorskiej, czyli gdy obraz jest pomniejszony, odwrócony i rzeczywisty jaad75 - Czw 30 Gru, 2010
cybertoman - Czw 30 Gru, 2010 jaad75, jesli 100% to dla Ciebie malo...
Nie marudze Panowie, ale skoro potraficie dyskutowac o 30 ISO przy 12800, czy spierac sie o pojedyncze pixele, to teorie o zaokraglaniu tu po prostu nie przystaja. jaad75 - Czw 30 Gru, 2010
Introverder - Pią 31 Gru, 2010 Temat postu: - A ja mam takie pytanie, oddałem kilka dni temu obiektyw do kalibracji (C 400/5.6L (do C 50D) bo mi ostrzył przed celem, minimalnie, ale jednak co przy zdjęciach ptaków z bliższej odległości było widoczne i dokuczliwe..), wczoraj go odebrałem. Pytanie tyczy się pewnej ciekawostki/"osobliwości", o ile jeszcze nie sprawdziłem dokładnie celności - na oko wydaje się być ok (parę zdjęć ze statywu robionych w domu), to zastanawia mnie czemu zanim oddałem obiektyw z aparatem do serwisu to konwerter naturalnie sprawiał, że aparat pokazywał światło f/8.0 (oczywiście z tym obiektywem), to teraz pokazuje mi f/5.6. A inne spostrzeżenie, to że chyba teraz obiektyw wraz z konwerterem (C 1.4 II, zaklejone styki..) jakby jest duużo bardziej czuły i lepiej wyłapuje w ogóle ostrość Jakość obrazu z konwerterem C 1.4 II jest b. dobra (na otwartej maksymalnie przysłonie) i nie ma żadnego widocznego spadku jakości komor - Pon 03 Sty, 2011
Może coś Ci się ze stykami porobiło i aparat nie załapuje faktu, że podpięty ma tandem szkło+TC. A co się pokazuje np. w Lightroomie (jeśli używasz)? Jako nazwa obiektywu powinno figurować: nazwa szkła + nazwa konwertera. Coś jak w ten deseń: 
cybertoman - Pon 03 Sty, 2011 Pozwole sobie wrocic jeszcze na chwile do pytania wyjsciowego. 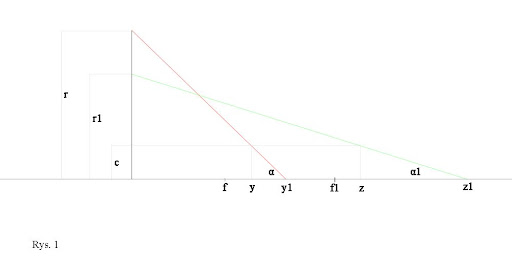
f, f1 - ogniskowe c - krazek rozproszenia r, r1 - promien otworu odpowiednio dla f i f1 y - odleglosc od soczewki ostrego obrazu punktu x przy ogniskowej f. y1 - odleglosc od soczewki punktu x1, wyznaczajacego GO przy ogniskowej f z - odleglosc od soczewki ostrego obrazu punktu x przy ogniskowej f1. z1 - odleglosc od soczewki punktu x1, wyznaczajacego GO przy ogniskowej f1 W pierwszym kroku spojrzmy, co dzieje sie przy wydluzeniu ogniskowej o wartosc n przy niezmienionej odleglosci x i x1. Jesli GO ma zostac zachowana, to wyglada to jak na rys. 1. Czyli: tg(a) = r/y1 = c/(y1-y) -> r = c*y1/(y1-y). tg(a1) = r1/z1 = c/(z1-z) -> r1 = c*z1/(z1-z). r/r1 = (c*y1/(y1-y))/(c*z1/(z1-z)) = (y1*(z1-z))/(z1*(y1-y)). Korzystajac z: 1/F = 1/X + 1/Y -> Y = F*X/(X-F) oraz f1 = n*f y = f*x/(x-f) y1 = f*x1/(x1-f) z = n*f*x/(x-n*f) z1 = n*f*x1/(x1-n*f) po podstawieniu r/r1 = ((f*x1/(x1-f))*((n*f*x1/(x1-n*f))-(n*f*x/(x-n*f))))/((n*f*x1/(x1-n*f))*((f*x1/(x1-f))-(f*x/(x-f)))) Zmudne skracanie podeslemy Wolframowi(mozna sprawdzic samemu wrzucajac skopiowane, powyzsze rownanie lub policzyc na piechote...), a ten twierdzi, ze: r/r1 = (n*(f-x))/(f*n-x) dla wygody zmodyfikujmy to tak: r/r1 = n * (x-f)/(x-f*n) dla x >> f, r/r1 = n Zblizajac sie z x do f stosunek ten bedzie coraz wiekszy. Zeszlo mi dluzej, niz myslalem i czas mi sie konczy, wiec napisze tylko, ze trzeba uwzglednic jeszcze zmiane GO przy zmianie wielkosci matrycy i zmiane otworu wzglednego wynikajaca ze zmiany ogniskowej, by uzyskac zadany wynik n*n/n = n. Dla n = √2 =ca 1.4 bedzie 1EV dla n = 2 to 2EV hijax_pl - Pon 03 Sty, 2011 cybertoman, chyba nie takie było pytanie początkowe Co do Twojego rozpisania, to prawdę mówiąc nie chce mi się sprawdzać wszystkiego po kolei, ale patrząc od drugiej strony klasyczne wzory na GO używają odległości hiperfokalnej i przedmiotowej. Rozpatrujemy przypadek gdy odległość przedmiotowa s >> f Hiperfokalna to nic innego jak zależność: H = f^2 / (N * c), gdzie f - ogniskowa, N - liczba przysłony, c - wielkość krążka rozproszenia. Jeśli zamienimy wartość przysłony na jej rozmiar bezwzględny, czyli N=f/d, otrzymamy: H = f*d/c Chcemy to samo GO przy zachowanym dystansie przedmiotowym czyli chcemy mieć tą samą hiperfokalną. Dodatkowo interesuje nas zachowanie dla tego samego rozmiaru otworu przysłony, czyli: f1*d/c1 = f2*d/c2 lub upraszczając f1/c1=f2/c2, gdzie f1,f2 dwie ogniskowe, c1 i c2 - dwa krążki rozproszenia Przyjmujemy, że relacja między ogniskowymi jest f2=f1*n, podstawiamy, i otrzymujemy: c2=c1 * n pitras - Pon 03 Sty, 2011
I dlatego wlaśnie czytam optyczne |