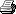maziek - Czw 12 Lut, 2009 Temat postu: Głebia ostrości - zależy od... Zabawiając się na tej stronie odkryłem że np. dla Nikona D80, D300 czy D700 podawany jest krażek rozproszenia 0,02mm a dla powiedzmy Canona 50D 0,019mm. Ta "niewielka" różnica powoduje spore konsekwencje, przykładowo dla odleglości przedmiotowej 10m (ogniskowa rzeczywista 50mm, f/8) całkowita głębia ostości Nikona i Canona to odpowiednio 21,4m i 19,1m zaś hiperfokalna to 15,7m i 16,5m. Z czego to wynika? Ten sam obiektyw i pozostałe parametry, GO powinna być identyczna. Gdyby chodziło o to, że zależnie od rzeczywistej rozdzielczości matrycy akceptowalna jest inna średnica krążka rozproszenia - to IMO D80, D300 i D700 powinny mieć tą średnicę inną. Czy też nie ma sobie czym głowy zawracać, rzecz polega na tym, że program oblicza GO ze wzoru do którego podstawiane są średnice krążka podawane np. przez producenta? Sprawa ma w sumie niewielkie znaczenie praktyczne, ale dlaczego tak? jaad75 - Czw 12 Lut, 2009 Po pierwsze, CoC dla D700 nie wynosi 0.02mm, tylko 0.03mm, a po drugie, wielkość CoC zależy od fizycznych rozmiarów matrycy. maziek - Czw 12 Lut, 2009 Czyli tam jest byk? W takim razie sprawa jest mocno teoretyczna. Domyślam się, że żywcem przeszczepiona z filmu analogowego? A czy w dobie cyfry średnica krążka nie powinna być uzależniona od fizycznego rozmiaru piksela (w jakis sposób, nie mówię że sztuka za sztukę)? Pytam w tym kierunku, że na wzmiankowanej stronie nie podaje się rozmiaru matrycy a typ aparatu, więc poniekąd rozumie się samo przez się, że pod ten typ aparatu (a więc i własciwości matrycy) obliczenie powinno być wykonane. Arek - Czw 12 Lut, 2009 Maziek, tutaj masz trochę wzorów: http://en.wikipedia.org/wiki/Depth_of_field palindrom - Czw 12 Lut, 2009 Na dobrą sprawę, CoC to "efektywna wielkość piksela", czyli jest zależna od ilości pikseli i wielkości matrycy (i pewnie demozaikowania  ).
Ta "niewielka" różnica to 5%. Pozory bywają mylące 
"Z czego to wynika? Ten sam obiektyw i pozostałe parametry, GO powinna być identyczna." Widać CoC rzeczywiście się różni. Tak na szybko, biorąc pod uwagę rozdzielczość poziomą: >> % Nikon D80 >> 23.6/3872 ans = 0.0061 >> % Nikon D300 >> 23.6/4288 ans = 0.0055 >> % Nikon D700 >> 36/4256 ans = 0.0085 Mają różne akceptowalne krążki rozproszenia
jaad75 - Czw 12 Lut, 2009
Tak, jest błąd - D700 ma dokładnie taki sam CoC jak D3.
Wg. mnie jednak nie należy brać pod uwagę rozdzielczości, bo CoC jest podawany dla określonych warunków wydruku. Zresztą, jak widać twórcy DoF Mastera też wychodzą z tego założenia, bo dla matryc tej samej wielkości podają ten sam CoC, mimo drastycznie różnych rozdzielczości... Rizzo - Czw 12 Lut, 2009 A jaki ma a900 Coc też 0,03? jaad75 - Czw 12 Lut, 2009
Tak. Rizzo - Czw 12 Lut, 2009 Dzięki mavierk - Czw 12 Lut, 2009 bo chyba to CoC mówi nam, jakim ułamkiem przyjętego za wzór obrazu jest matryca. Czyli będzie zależne to tylko od rozmiarów matrycy, natomiast nie od jej rozdzielczości. maziek - Czw 12 Lut, 2009 Chyba (na ile pamietam) chodzi o to, jaka plamka będzie jeszcze widziana na odbitce jako punkt. To zalezy poniekąd od umowy, jakich rozmiarów odbitki z jakiej odl. sie ogląda. Więc w porządku, na tej zasadzie umawiając się to ta plamka będzie miała średnicę określoną ściśle jako ułamek matrycy, ale jeśli piksel matrycy jest większy niż tak określona plamka to PRAKTYCZNIE sprawa traci sens, ponieważ dla takiej matrycy głębia ostrości będzie PRAKTYCZNIE wieksza (PRAKTYCZNIE tzn. w sensie w jakim przedziale odległości punkty obrazu są na matrycy plamkami nie większymi od piksela). palindrom - Czw 12 Lut, 2009 No i mamy kilka poprawnych definicji
Faktycznie jest tak, że oko w plamce żółtej ma rozdzielczość kątową ok. 1', co można przełożyć na rozmiar krążka na np. odbitce 18x13 w odległości dobrego widzenia. Dodatkowo gdy takie zdjęcie było robione obiektywem ~50mm dostaniemy ekwiwalent tego, co byśmy widzieli gołym okiem. Widać tym się kierowali wyznaczając DOF. W sumie to logiczne, chyba że chcemy robić crop ze zdjęcia, wtedy CoC będzie mniejszy. Skrajnie - piksel na matrycy / statystyczny rozmiar kryształka halogenku srebra. maziek - Wto 17 Lut, 2009 Tak jeszcze chodze koło tego i powoli dochodzę do wniosku, że w praktyce wygodniej byłoby uzależniać GO od średnicy krażka rozproszenia wielkości elementarnego elementu światłoczułego. Gwarantowałoby to wykonanie zdjęcia przy maksymalnej mozliwej na danym detektorze ostrości o głebi od-do metrów. Na analogu jest to raczej zbyt skomplikowane (rózne filmy plus jeszcze różna obróbka) ale na cyfrze to tak powinno być zrobione. palindrom - Wto 17 Lut, 2009 maziek, ale ja to w pierwszym poście na tej stronie napisałem 
Jeżeli o kliszę chodzi, to jest to możliwe, choć niewygodne. W dobrej kliszy kryształki halogenków srebra mają przekrój czynny w okolicach 2µm ale w materiałach o wyższej czułości jest różnie. Z resztą wielkość ziarna trzeba odróżnić od rozmiarów kryształków... Tia. Lepiej użyć rozdzielczości oka
maziek - Wto 17 Lut, 2009 Ja to muszę kilka razy przeczytać, zanim dotrze .
mavierk - Sro 18 Lut, 2009 ale ten krążek rozproszenia ma tak nikłe znaczenie, ze nie warto się nim w ogóle interesować 
maziek - Wto 24 Lut, 2009 Praktycznie to jak kto lubi może się interesować, albo nie. Teoretycznie to ja lubię wiedzieć .
Palindrom, a co by było, gdyby założyć, że mamy idealny możliwy (fizycznie) obiektyw i idealną matrycę o maksymalnej możliwej (fizycznie) rozdzielczości (idealną w sensie, że nie cierpiącą na przypadłości gęsto upakowanych matryc). Czy jest możliwe, aby średnica krążka rozproszenia była limitowana nie własnościami matrycy a dyfrakcją na obiektywie? palindrom - Sro 25 Lut, 2009 maziek, no to zobaczmy
Korzystam z kryterium Rayleigh'a: >> % Weźmy obiektyw 50/2. Apertura ma średnicę 25mm >> dl = 1.22 * 550e-9 * 50e-3 / 25e-3 dl = 1.3420e-06 >> % Idealny obiektyw 50/2 daje krążek Airy'ego 1.342µm To znaczy że piksele muszą być mniejsze niż 1.3µm, najlepiej kilkukrotnie, żeby matryca była zdolna zebrać obraz generowany takim idealnym obiektywem. A właściwie czy jest sens przy odbitkach 18x13?... - A niech będzie że to na APS-C się dzieje i powiększamy do 18x13, czyli liniowo z 25mm do 180mm - 7.2x Krążek ma rozmiar 9.6624µm - Obserwujemy odbitkę z "odległości dobrego widzenia" - 25cm >> 9.6624e-6/25e-2 % To rozmiar kątowy w radianach ans = 3.8650e-05 >> ans*180/pi % To rozmiar kątowy w stopniach ans = 0.0022 >> ans*60 % To rozmiar kątowy w minutach ans = 0.1329 Nasze oczy mają rozdzielczość o rząd wielkości gorszą
maziek - Sro 25 Lut, 2009 Krótko mówiąc (o to mi chodziło) fizyczne ograniczenie "od dołu" głebi ostrości istnieje ze względu na własności samego obiektywu. Czyli biorąc pod uwagę doskonały obiektyw i idealną matrycę i tak będzie istniała jakaś głębia ostrości różna od zera. Dość niesamowite stwierdzenie jak się zastanowić. Dzieki za starunek  .
komor - Sro 25 Lut, 2009 Głębia ostrości różna od zera? Thanks god! Inaczej wszystko byłoby rozmyte.
A tak na poważnie, Maziek, to nie bardzo rozumiem w sumie co drążysz. Głębia ostrości, z tego co rozumiem, nie jest fizycznie ścisłym pojęciem, tylko uzależnionym właśnie od naszego postrzegania, stąd uwzględnia się przeciętne oko i oglądanie obrazu z określonej odległości przez człowieka. Krążek rozproszenia z definicji to potwierdza, bo nie definiuje on jak jest dobrze, tylko na ile jest źle bo się rozprasza.
Kręcę coś?
maziek - Czw 26 Lut, 2009 Drążę z ciekawości. Chyba nic nie kręcisz. Tak mi się zdaje, że podchodząc do sprawy maksymalnie klasycznie (geometrycznie) ostrość idealna może być tylko "w punkt" czyli GO=0. Zaś z tego co napisał Palindrom wynika, że w realnym świecie jakby sie nie starać to mamy ze wzgledu na ograniczenia samego obiektywu niezerową GO wewnątrz której jest "możliwie najmniej nieostro" (a wcale nie "ostro"). Dla mnie praktyczne znaczenie ma uświadomienie sobie, jak bardzo arbitralne są te tabelki z obliczniem GO. Natomiast chciałem jeszcze podpytać mądrzejszych o kształt GO. Z tego co kiedyś czytałem są obiektywy, w których płaszczyzna ostrości nie jest płaszczyzną a wycinkiem sfery (czy jakąś inną krzywizną)? komor - Czw 26 Lut, 2009 Z tym GO=0 to rzeczywiście problem. Ale z tego co pamiętam że czytałem to falowa natura światła powoduje, że nie ma takiego czegoś jak idealne trafianie w punkt z idealnie małym promieniem światła. Może Palindrom lub Arek napiszą coś sensownego. maziek - Czw 26 Lut, 2009 To na pewno z powodu falowej natury. Chodzi mi o to, że jest to niejako sprzeczne z "chłopskim rozumem". Komor, jak to sie kiedyś mawiało MSPANC: masz strasznie uduchowionego awatara . Zupełnie jakbyś własnie do I komunii szedł .
mavierk - Czw 26 Lut, 2009 a mi się zdaje, że istnieje moment w którym ostrość kończy się szybciej, niż zaczyna i mamy taki konflikt interesów
palindrom - Czw 26 Lut, 2009 W podejściu geometrycznym istnieje odwzorowanie punkt w punkt i jest on nieskończenie mały. W świecie realnym jest dyfrakcja i wiązki gaussowskie, więc "punkt" jest odwzorowany w plamkę. To wszystko nie ważne, gdyż pojęcie głębi ostrości wymaga zdefiniowania największej plamki, która jest jeszcze interpretowana jako punkt, tak więc nawet gdy weźmiemy podejście geometryczne, będziemy mieli niezerową głębię ostrości. komor, dzięki dyfrakcji mamy plamki Airy'ego zamiast punktów, co nie zmienia faktu że żeby otrzymać najmniejszą plamkę, trzeba trafić w punkt (w przypadku światła i tak nie ma sensu definiować punktu mniejszego niż 0.5µm )
maziek, w absolutnie żadnym obiektywie płaszczyzna obrazowa nie jest płaszczyzną Istnieje krzywizna pola, której wielkość bardzo często jest podawana wraz z wielkością astygmatyzmu. Pole obrazu jest na krawędziach zakrzywione w stronę układu optycznego. To skutek tego samego zjawiska jakie powoduje astygmatyzm - geometria układu, widziana przez światło padające z różnych punktów pola widzenia, jest inna. Oczywiście można ją "spłaszczać" ale nie ma układów optycznych pozbawionych wad.
Z resztą po co skupiać w punkt, skoro filtr AA i tak to zepsuje?
Poniżej przykłady punktowej funkcji rozmycia różnych układów. 7. jest bliskie ideału, a 8. pokazuje co z tym prawie ideałem robi filtr AA: 
Źródło: www.zeiss.de/C12567A8003B...F_Kurven_EN.pdf novy - Nie 04 Sty, 2015 Nie jarze jednego. Z tego co tu pisaliście CoC ma znikome znaczenie. W DOFMAster wpisuje 200mm f/2.8 10 metrów i dla 5D mam DoF Total: 0.42m a dla 40D 0.26m. Dlaczego różnica jest taka duża? dcs - Nie 04 Sty, 2015 Bo inna skala odwzorowania. hijax_pl - Nie 04 Sty, 2015
Matematycznie to będzie tak: matryca 5D ma poziomy rozmiar 36mm, by uzyskać rozmiar 30cm należy użyć skali 300/36 = 8.3. Dla aparatu 40D będzie to odpowiednio 300/22=13.6. Stosunek wzajemny tych dwóch współczynników powiększeń to 13.6/8.3=1.6 (chyba już kojarzysz co to za współczynnik )
No, to skoro przyjmuje się, że dla aparatu pełnoklatkowego krążek rozproszenia by był niewidoczny musi być nie większy nić 0.03 mm to znaczy, że jego odpowiednik dla 40D będzie 0.03/1.6 = 0.02 mm Stąd ta różnica w CoC, którą trzeba uwzględnić we wzorze. novy - Pon 05 Sty, 2015 Dzięki za wyjaśnienie. Nigdy w sumie nie pomyślałem o tym że DOF zależy od powiększenia, ale jest to jasne. Z tego wynika że jeśli patrze na zdjęcie w powiększeniu 100% na monitorze to DOF jest dużo mniejsze niż to które jest podawane w DOFMaster. komor - Pon 05 Sty, 2015
Dość łatwo sprawdzić to organoleptycznie. Wystarczy nieco mydlane w 1:1 zdjęcie zmniejszyć na ekranie do na przykład 25% i od razu wydaje się ostrzejsze. To dotyczy też przecież głębi ostrości, czyli tego co uznajemy za jeszcze ostre, a nie rozmyte. |
